Das R-Paket ForestElementsR als forstlicher Taschenrechner - Eine Schritt-für-Schritt-Einführung
von Peter Biber, Astor Toraño Caicoya und Hans-Joachim Klemmt

R lädt das Paket von CRAN und installiert es mit allen anderen dafür benötigten Paketen, falls diese noch nicht vorhanden sind.

Wenn R gestartet ist, ist eine Eingabe an der Kommandozeile im „Taschenrechner-Stil“ der einfachste Weg, der Software Befehle zu übermitteln. Eine einfache Rechenoperation wäre wie folgt einzugeben

und würde zu folgender Antwort führen:

Möglich sind auch komplexere Eingaben; z.B. stellt der Befehl

die mathematische Funktion y=sin(x²) im Bereich −3<x<3 in roter Farbe graphisch dar:

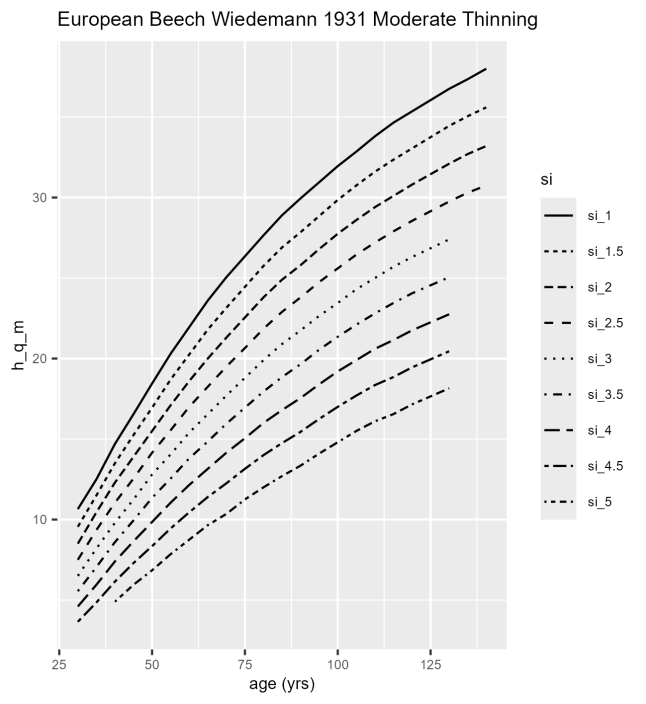
Abb. 1. Mit ForestElementsR erzeugte Darstellung des Bonitätsfächers der Ertragstafel für Rotbuche, mäßige Durchforstung, von Wiedemann (1931) (BaySTMLF 2018). Die horizontale Achse zeigt das Bestandesalter, die vertikale Achse die Höhe des Grundflächenmittelstammes. Mit „si“ ist der international übliche Begriff für die Bonität, „Site Index“ abgekürzt. Die mit „si_1.5“ bezeichnete Kurve stellt also die Höhenentwicklung bei einer Bonität von I.5 dar.

Die konkrete Bonität (international „Site Index“) des Bestandes erhalten wir mit dem Befehl site_index() unter Angabe von Alter (57 Jahre), Mittelhöhe (20.0 m) und der gewünschten Ertragstafel:

Der Bestand hat also eine Bonität von rund I.3; diese Information haben wir in der Variable „bon“ abgelegt. Zusammen mit dem Alter kann sie verwendet werden, um die zugehörigen Werte beliebiger Variablen aus der Ertragstafel zu ziehen. Dazu dient die Funktion ytable_lookup(), mit der wir hier den laufenden Zuwachs des Bestandes (im Paket mit der international üblichen Abkürzung „pai“ bezeichnet; „pai“ = „periodic annual increment“) schätzen wollen:

Laut Ertragstafel ergibt sich so für den Bestand ein Zuwachs von rund 11,6 Festmetern pro Jahr und Hektar, s. allerdings die Anmerkungen zur Zuwachsschätzung mit Ertragstafeln von Pretzsch in BaySTMELF (2018), wo für die Buche eine Korrektur von +20% vorgeschlagen wird. Aus Gründen des Umfangs kann hier nicht weiter auf die Handhabung von Ertragstafeln mit ForestElementsR eingegangen werden. Interessierte Leser seien auf die ausführliche Darstellung in der entsprechenden Vignette des Paketes hingewiesen:

Yield Tables in ForestElementsR

Das Paket ForestElementsR ermöglicht auch erste Auswertungen zur Baumart- und Strukturdiversität von Beständen namentlich des in der Ökologie weit verbreiteten Diversitätsindex von Shannon (1948) und des Artprofilindex von Pretzsch (2019). Letzterer beruht auf dem gleichen Prinzip wie der Shannon-Index, bezieht aber auch noch die Komponente der vertikalen Bestandesstruktur ein. Zum Einsatz solcher Indizes bei der Abschätzung von Ökosystemleistungen s. Biber et al. (2020, 2021), Blattert et al. (2017) und Brockerhoff et al. (2017). Im Folgenden berechnen wir beide Indizes für unseren Beispielbestand. Hierfür ist es notwendig, für jeden einzelnen der elf Bäume die Baumart explizit anzugeben, auch wenn es sich um einen Buchenreinbestand handelt. Wir müssen also den Baumartencode 60 (s.o.) elfmal wiederholen und den erhaltenen Vektor als Baumartencodes nach dem System der Bayerischen Staatsforsten definieren:

Den Shannon-Index erhalten wir mit der Funktion „shannon_index“, die neben dem Vektor mit den Artcodes auch die Repräsentationszahlen der einzelnen Bäume, „n_rep“, als Angabe benötigt:

Da wir es mit einem Reinbestand zu tun haben, ist die Baumartendiversität folgerichtig 0. Der Artprofilindex (Funktion „species_profile“) benötigt als Eingangsinformation zusätzlich noch die Höhen der Bäume (die wir zuvor in der Variable „h“ abgelegt haben):

Der erhaltene Wert ist größer als Null, weil der Bestand zwar ein Reinbestand, aber nicht völlig einschichtig ist. Zum Vergleich nehmen wir nun an, dass nicht alle unserer Bäume Buchen, sondern drei davon Eichen (Code 70) und einer davon eine Kiefer (Code 20) ist. Entsprechend definieren wir einen zweiten Vektor mit Baumartenbezeichnungen:

Dies führt erwartungsgemäß zu einer deutlichen Anhebung beider Indexwerte.

Im Rahmen dieser Einführung kann nicht näher auf die Funktionsweise dieser Indizes eingegangen werden; eine gut verständliche Darstellung findet sich jedoch in Pretzsch (2019). Eine wichtige Anwendung besteht darin, dass bei der Auswertung von Folgeaufnahmen durch den Vergleich dieser Indexwerte festgestellt werden kann, in welche Richtung sich die Art- und die Strukturdiversität entwickeln.